Leçons du chapitre

Écriture d’un entier positif dans une base

I. Introduction : Le Principe des Bases Numériques

A. Le Système Décimal (Base 10) : Décomposition Positionnelle

Le système décimal utilise 10 chiffres (0-9). La valeur d'un nombre est donnée par la somme des chiffres multipliés par la puissance de 10 correspondante à leur position.

Formule générale :

(ck−1ck−2…c0)10=ck−1×10k−1+…+c1×101+c0×100(c_{k-1} c_{k-2} \ldots c_0)_{10} = c_{k-1} \times 10^{k-1} + \ldots + c_1 \times 10^1 + c_0 \times 10^0

B. Les Bases Informatiques Clés

L'informatique utilise principalement les bases liées à 2: Binaire (b=2), et Hexadécimal (b=16).
Base (b) Nom Chiffres Poids de position
2 Binaire 0, 1 Puissance de 2
10 Décimal 0 à 9 Puissance de 10
16 Hexadécimal 0-9, A-F Puissance de 16
(Rappel : A=10, B=11, C=12, D=13, E=14, F=15)

II. Conversion Binaire <-> Décimal (2<->10)

A. De Binaire vers Décimal (2 -> 10)

On utilise la décomposition positionnelle par les puissances de 2 (Méthode vue précédemment).

Exemple :

(1101)2=1×23+1×22+0×21+1×20(1101)_2 = 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^01×8+1×4+0×2+1×1=8+4+0+1=(13)101 \times 8 + 1 \times 4 + 0 \times 2 + 1 \times 1 = 8 + 4 + 0 + 1 = (13)_{10}

B. De Décimal vers Binaire (10 -> 2)

On utilise les divisions successives par 2.

Exemple :

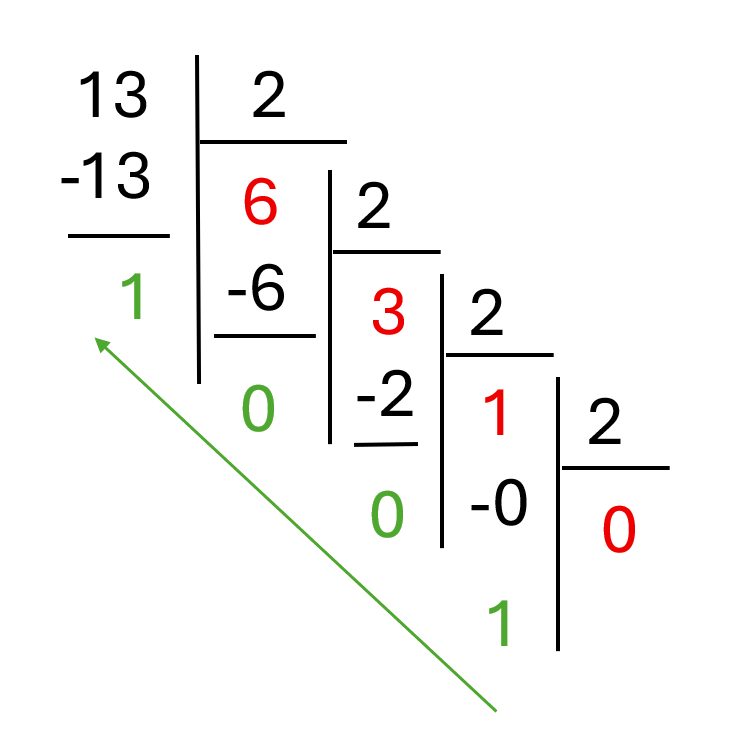
Convertir (13)10.

illustration

III. Conversion Hexadécimal <-> Binaire (16 <-> 2)

C'est la conversion la plus rapide en informatique car 24 = 16. Un chiffre hexadécimal correspond exactement à un groupe de quatre bits (quartet ou nibble).

A. De Hexadécimal vers Binaire (16 -> 2)

On remplace chaque chiffre hexadécimal par son équivalent binaire sur quatre bits.

Exemple :

B=(11)10→(1011)2B = (11)_{10} \to (1011)_2

9=(9)10→(1001)29 = (9)_{10} \to (1001)_2

Résultat : (1011 1001)2(1011 \ 1001)_2

B. De Binaire vers Hexadécimal (2 ->16)

  1. On divise le nombre binaire en groupes de quatre bits à partir de la droite. (Ajouter des zéros non significatifs à gauche si nécessaire).
  2. On convertit chaque quartet en son chiffre hexadécimal équivalent.

Exemple :

    Convertir (1010110)2(1010110)_2

    1. Grouper par 4 (en partant de la droite) : 0101 | 0110 (Le premier groupe a été complété par un zéro à gauche).
    2. Convertir :
      • (0101)2  = 5
      • (0110)2 = 6
    Résultat : (56)16

IV. Conversion Hexadécimal <-> Décimal (16 <-> 10)

A. De Hexadécimal vers Décimal (16 -> 10)

On utilise la décomposition positionnelle par les puissances de 16.

Exemple :

Convertir (1A)16. (1A)16 = 1 x161 + A x 160 1 x 16 + 10 x1 = 16 + 10 = (26)10

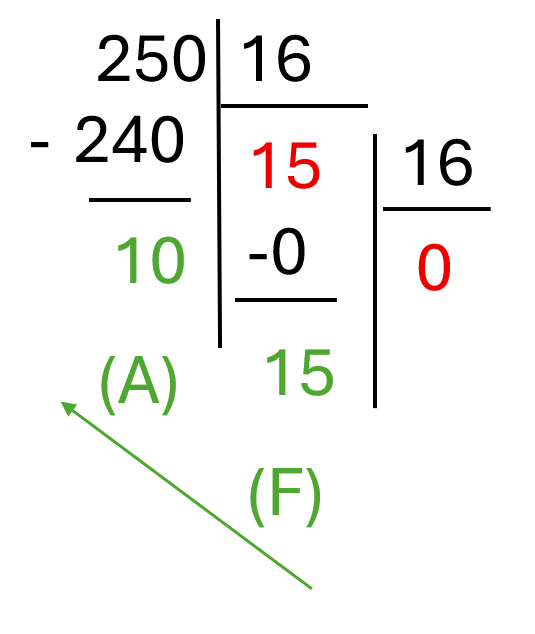
B. De Décimal vers Hexadécimal (10 -> 16)

On utilise les divisions successives par 16.

Exemple :

Convertir (250)10 en base 16.

Exercices

Fiches de révision

Numération et Bases